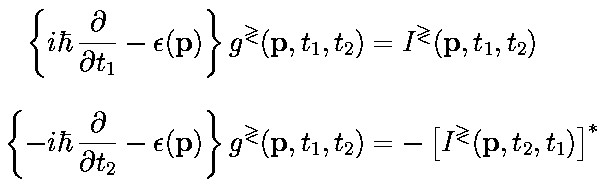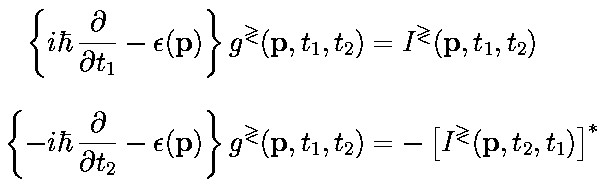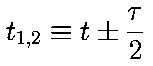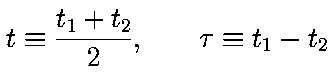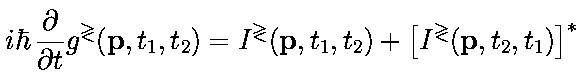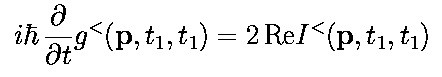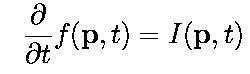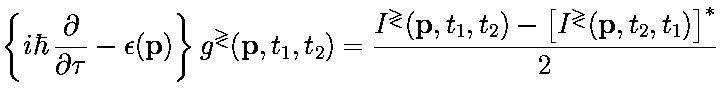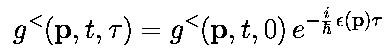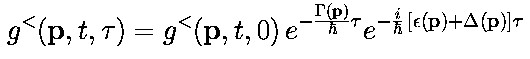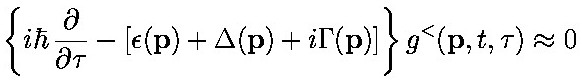Kadanoff-Baym equations

Aim: give a consistent description of electron relaxation and energy renormalization
In contrast to free electrons which are characterized by an undamped electron DeBroglie wave, correlations lead to damping
To see the damped spectral functions, click here

Kadanoff-Baym equations for an electron gas

Equations of motion for the two-time correlation functions.
The g's have to obey the adjoint equation (second equation) also.
The I's are the scattering (collision) integrals containing the influence of all other particles.

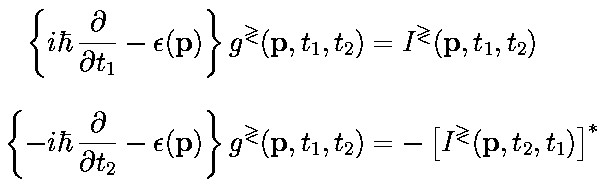
Relation to the center of mass and difference time, t and tau

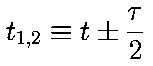
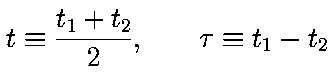
Relation of g< to the electron (Wigner) distribution function

On the time-diagonal, g is essentially the Wigner function.
Consider the difference of the two KB equations above
The equal time limit (second equation below) is just the kinetic equation for the Wigner distribution (third equation below) - you only need to identify f and I.

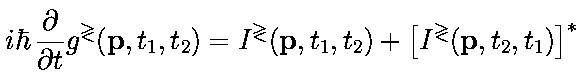
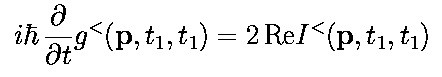
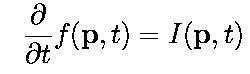
Additional information in the Green's functions

Due to the two-time structure, the g's contain essentially more information than the single-time Wigner distributions.
Besides this statistical information, they contain the full dynamic properties - the energy spectrum - which is reflected by the behavior away from the time-diagonal
Consider the sum of the two KB equations above:

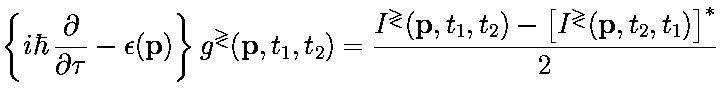
Solution for free particles (I=0):

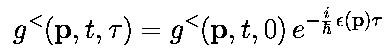
For interacting particles expect the generalization:

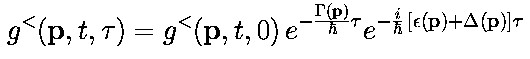
which corresponds to an equation with an "effective" (complex) energy - which is a simple special case of the above equation.

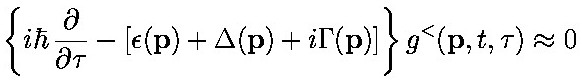
Thus, the Kadanoff-Baym equations yield the renormalized single-particle spectrum, fully selfconsistently. To see the corresponding spectral functions, click here

Idea of nonequilibrium Greens functions
See time-dependent solutions | Results for optically excited electrons in semiconductors
Back to main page | Hauptseite