How to determine Fermi vectors by angle resolved photoemission?

A new method for the determination of Fermi vectors from photoemission spectra is presented. It produces Fermi surfaces with high accuracy and reliability even for narrow band systems.
A wide variety of physical phenomena of materials rely on details of the topology of the Fermi surface. However, traditional experimental determinations are restricted to bulk materials. More complex cases, such as superlattices, heterostructures or even clean surfaces can hardly be accessed. In such situations, angle-resolved photoemission spectroscopy (ARPES) has recently been extensively applied to gain insight into the topology of Fermi surfaces.
Spectra Fermi vectors have been extracted from experimental ARPES data like those shown on the left, employing three kinds of criteria,

maximum ARPES intensity at the Fermi level,
maximum gradient of the energy integrated photoemission intensity, the gradient taken with respect to the wave vector, or
fitting ARPES peak positions over several emission angles and extrapolating the dispersion to the Fermi level.
However, none of these techniques explicitly considers the detailed mechanism of the photoemission process, and the accuracy of the determination has never been questioned. It turns out that there are problems even for extensively studied cases. If photoemission calculations including the complete physics (within the one-step model) are not available, practical procedures for an analysis of high resolution photoemission data are needed.
Such a method is presented here as a result of a strong collaboration between experiment and theory. The new method had to be simple and stable for the necessities of the measurement and reliable from a theoretical point of view. Employing high resolution photoemission spectroscopy we show how surface-parallel components of the Fermi vectors can be determined with high accuracy. Intensity modifications due to the photoemission process are explicitly eliminated by comparing photoemission spectra taken at different temperatures.
If from one of the other methods a rough estimate is known, the Fermi vector can accurately be fixed by subtracting the photoemission intensities for two temperatures. If taken at the Fermi level for different wave vectors in the neighborhood of the estimate, the vanishing of the difference determines the Fermi vectors. This is valid for a variety of spectral functions, including Lorentzians, Gaussians, Voigt profiles, the Luttinger model, a refined Luttinger profile, two dimensional and marginal Fermi liquids.

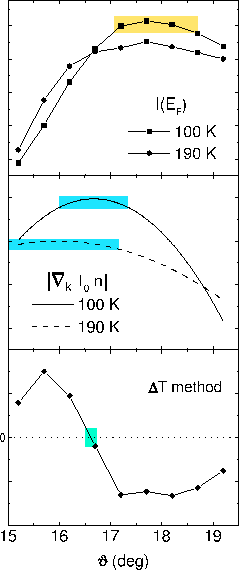
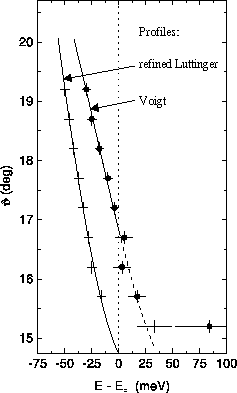
Fig. 1: Angle resolved photoemission spectra associated with the Ti 3d-band of 1T-TiTe₂ in the Gamma-M direction were taken at 100 K and 190 K.
Left: (top ) Intensities at the Fermi level (maximum-intensity method). Yellow bar marks the uncertainties for the parallel part of the Fermi vector (95% of the maximum value).
(middle) Smoothed k-derivatives of the intensities integrated over the whole spectra (maximum-gradient method). Blue bars mark the uncertainties as above.
(bottom) Difference of the two intensities at the Fermi level. The intersection with zero marks the Fermi vector. The green bar shows the uncertainty of 0.1° which emerges from the error of the Fermi energy (1 meV).
Right: k_F determination from extrapolation of fitted peak positions using two different profiles.

For an application of the new method we study normalized photoemission spectra of the layered material 1T-TiTe₂, taken at 100 K and 190 K. The high energy and angle resolved spectra along the Gamma-M direction contain the peaks emerging from the Ti 3d-band, which is well separated from contributions of other bands.
Intensities at the Fermi level are depicted in Fig. 1, top left. According to the new method the Fermi vector is given by the intersection of the curves, which can clearly be identified at a value of 16.6°, see the difference of the spectra at the bottom of the left panel.
For comparison we also show the values obtained from the maximum intensity (top) and maximum gradient (middle) methods as described above. The maximum intensity at the Fermi level can be observed on a relatively broad peak at around 17.8°, showing a systematic erroneous shift towards occupied states. The derivative of the energy integrated intensities are depicted in the middle of the left panel. Since the gradient of the integrated intensity is only marginally changing in the regime of interest a rather broad maximum is observed making a detailed quantitative analysis difficult. In the right panel estimates from the peak-tracing method for two assumed profiles are shown. With a Voigt profile the Fermi vector appears at 16.7° and with a refined Luttinger profile at 14.75°.
See also:

L. Kipp, K. Roßnagel, C. Solterbeck, T. Strasser, W. Schattke, M. Skibowski, How to Determine Fermi Vectors by Angle Resolved Photoemission?, Phys. Rev. Lett. 83, 5551 (1999); see also cond-mat/9905400
Acknowledgment: This research is supported by the BMBF, FR Germany (project No. 05 SB8 FKB, 05 SE8 FKA and 05 SB8 FKA).

1999 Claus-Henning Solterbeck

CAU Kiel Physics Theory Home Highlights 24 Feb 2000