Elektronische Struktur von Festkörpern
Die Struktur der festen Körper, so wie sie sich dem unbewaffneten Auge
darbietet oder in den Materialeigenschaften der täglichen Erfahrungswelt
niederschlägt, ist fast ausschließlich durch die
Bindungsverhältnisse
der Elektronen im atomaren Bereich festgelegt. Daher kommt der Untersuchung
der elektronischen Struktur eine hervorragende Bedeutung in der
Festkörperphysik zu. Schließlich war und ist sie auch die Grundlage, die die
technische Entwicklung auf elektronische Bauelemente immer kleinerer
Größenskala führt und die - obwohl kaum wahrgenommen - in
keiner Weise
mehr aus dem heutigen Leben wegzudenken ist.
Mit der gegenwärtig vorhandenen Leistungsfähigkeit der Superrechner
ist
man in der Lage, Festkörperstrukturen aus ersten Prinzipien, d.h.
ohne Rückgriff auf Messungen, zu bestimmen. Man erreicht dabei hohe
Übereinstimmung mit experimentellen Daten. Es verbleibt dem
Experiment jedoch eine
entscheidende Aussagekraft, da sich mit zunehmender
Feinheit der Methoden immer weitere Details offenbaren, die in den
theoretischen Untersuchungen zunächst mit Recht vernachlässigt worden
waren. Andererseits benötigt ein tiefes
Verständnis gerade dieser genauesten Messungen eingehende
theoretische Unterstützung. In dieser Kombination hat die
Vorhersagbarkeit von Eigenschaften neuer maßgeschneiderter
Materialien einen hohen Standard erreicht und beeinflußt damit die
Entwicklung bereits in deutlicher Weise. Unsere
Arbeiten betreffen alle diese zentralen quantenmechanischen Fragen
zur elektronischen Struktur
konkreter Materialien und zum Verständnis der zugehörigen Experimente.

Grundlagen
Als ein wichtiges Ziel und als Grundlage für weiterreichende Arbeiten
wird die elektronische Struktur der untersuchten Substanzen berechnet.
Den wichtigsten Zugang bildet die sogenannte Bandstruktur, in der die
möglichen Energien der Elektronen geordnet werden. Je nach Bedarf stehen
dafür unterschiedliche Verfahren zur Verfügung, von allgemeinen und
hochgenauen Programmen1, die einen hohen Aufwand erfordern,
bis zu speziell angepaßten schnellen Lösungen2-5.
Diese Techniken und Programme
werden beständig weiterentwickelt, um neue Aufgaben zu
erfüllen, die
durch die Anwendung auf neue komplexe Substanzklassen, auf Oberflächen oder
auch durch den Bedarf an höchster Genauigkeit entstehen
Ein weiteres Beispiel
ist die Berechnung angeregter elektronischer Zustände mit besonderen
Randbedingungen6-9.
Dazu mußten leistungsfähigste Verfahren
kombiniert und weiterentwickelt werden, um eine praktikable Lösung zu
liefern. Zu solchen
Aufgaben fürt auch die Frage nach der Reaktion eines Kristalls auf
elektromagnetische Felder. In der klassischen makroskopischen Welt ist
das als Induktion gut bekannt, die Erweiterung auf den mikroskopischen
quantenmechanischen Tensor der dielektrischen Funktion erfordert dagegen
sehr aufwendige Rechnungen10-13.
All solche eher unüblichen Anstrengungen sind
aber gerade wichtig für einen erfolgreichen Vergleich mit experimentellen
Ergebnissen 14,15.

Verständnis
Die experimentelle Bestimmung der elektronischen Struktur gelingt mit
der Photoemissionsspektroskopie. Dabei regt einfallendes Licht im Kristall
Elektronen an, die dann austreten und gemessen werden können. Unter
kontrollierten Versuchsbedingungen kann dann von diesem Photostrom
auf den Anfangszustand der Elektronen geschlossen werden.
Eine solche Auswertung ist anspruchsvoll. Höchstgenaue experimentelle
Aussagen sind im Moment nur aus dem Vergleich der gemessenen Spektren
mit den Rechnungen möglich. Die genauesten Rechnungen erlaubt derzeit die
Theorie des Einstufenmodells 16, das wegen des hohen
Aufwandes nur
wenige andere Gruppen auf der Welt anwenden.
Zum tieferen Verständnis der
Spektren existieren in der Theorie weitere Hilfsmittel zur Beschreibung
bestimmter Aspekte der elektronischen Struktur und der Prozesse der
Anregung und der Elektronenemission. Mitunter ist es nur damit
möglich, die Photoemissionspektren zu verstehen und mit der zugrunde
liegenden elektronischen Struktur zu verbinden.
Dieses theoretische Handwerkszeug erweist sich gerade bei der Anwendung
der Photoemission auf große Rekonstruktionen von Oberflächen, auf
bedeckte
Oberflächen und auf komplett neue Materialien als sehr fruchtbar und
derzeit konkurrenzlos leistungsfähig17.

Vollständige Information
Anstatt wie bislang üblich Photoströme in nur einzelne
wenige Raumrichtungen zu messen, werden in jüngster Zeit teilweise auch
alle Richtungen simultan berücksichtigt, was durch die Entwicklung neuer
Elektronendetektoren begünstigt wurde.
Der in diesen Intensitätsverteilungen
auftretende Reichtum an Informationen, der sich in der Energie- und der
Winkelabhängigkeit verbirgt, ist noch nicht vollständig und
systematisch
erschlossen. In den ersten Berechnungen solcher vollen Winkelverteilungen
überhaupt, siehe Abb. 1, wurde am Beispiel der
Si(001)-Oberfläche
der Einfluß der elektronischen Struktur und des einfallenden Lichtes
diskutiert18. Die Möglichkeiten zur Bestimmung der
Bandstruktur sind bei
diesen vollen Winkelverteilungen mit der Hoffnung verbunden, eine
leistungsfähige Methode zur direkten Abbildung
der sogenannten Fermiflächen zu entwickeln.
Diese Größe ist wichtig für das Verständnis vieler
elektronischer
Anregungen im Festkörper. Zugehörige Intensitätsverteilungen
wurden für
TiTe2 studiert, in Ergänzung zu den Untersuchungen der
Vielteilcheneffekte in diesem System19. Die Leistungsfähigkeit
der Winkelverteilung zur Bestimmung der elektronischen Struktur konnte
am Beispiel von GaAs(110) demonstriert werden: kleine Änderungen in
der Bindungsenergie erzeugen starke Variationen in dem Abbildungsmuster
der Photoströme20,21.
Umgekehrt kann diese Empfindlichkeit zur
genauen Eichung der Energieskala verwandt werden.
An dieser Substanz wurden auch weitere Informationen, die in den
Winkelverteilungen enthalten sind, zugänglich gemacht. Das betrifft Fragen
nach der räumlichen Herkunft und weiteren Eigenschaften der
Elektronen21,22.
Dieses Verständnis eröffnet neue Möglichkeiten für die
Anwendung der
Photoemission zur Untersuchung der elektronischen Struktur.
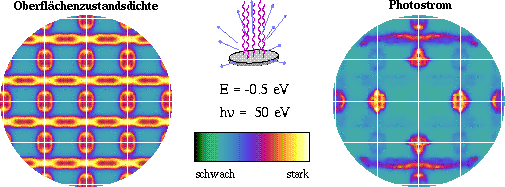
Abb. 1: Vergleich der elektronischen Struktur mit dem resultierenden
Photostrom. Die sogenannte Zustandsdichte links ist hier die geeignete
physikalische Größe zur Beschreibung der elektronischen Struktur. Der
daraus entstehende Photostrom sieht deutlich anders aus. Dennoch gelingt es,
aus den Photoströmen die Struktur links zu rekonstruieren und weitere
Informationen zu extrahieren. Die Skizze in der Mitte veranschaulicht den
physikalischen Prozeß: Licht trifft auf eine Materialprobe und regt
Elektronen an, die den Kristall verlassen und gemessen werden können.

Wechselwirkungen
Ein weiterer Schwerpunkt der Untersuchungen liegt in der Frage,
wie bei der heutzutage erreichten Genauigkeit die i.a.
vernachlässigte, allenfalls äußerst grob berücksichtigte
Wechselwirkung
der Elektronen untereinander zu behandeln ist.
Dieses Problem ist z.B. zentral
für den Magnetismus, die konventionellen sowie neuen Spielarten der
Supraleitung und ist in dem letztgenannten Beispiel noch weit von einer
quantitativen Lösung entfernt. So agieren die Elektronen in kollektiver
Weise und schirmen z.B. an Oberflächen die elektromagnetischen Felder der
Lichtwellen und selbst das Coulombfeld der bei der Photoemission
austretenden Elektronen auf komplizierte Art ab.
Will man die richtigen,
d.h. gemessenen, Intensitäten des Photostroms berechnen und damit auch
verstehen können, so müssen diese Effekte berücksichtigt
werden16. Im Fachjargon der Vielteilchenphysik
heißt das die Mitnahme von Selbstenergie- und Vertexkorrekturen.
Tatsächlich
sind die dadurch verursachten Änderungen in einem Photoemissionsspektrum
von der Größenordnung eines halben Elektronenvolts,
s. Abb. 2, und
damit für diesen Bereich der Physik gravierend14,19,23,24.
Die Diskussion solcher Effekte kann jetzt erst beginnen, da bislang
diese Rechnungen einmalig sind.
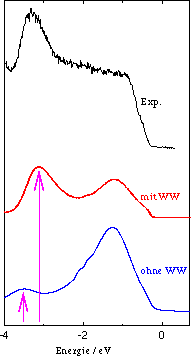
Abb. 2: Vergleich der gemessenen und berechneten
Photoströme für
TiTe2 (aus: Ref. 19). Unter der Messung sind
die Rechnungen mit und ohne
Wechselwirkungskorrekturen dargestellt. Ein Maximum wird durch diese
Einflüsse um 400 meV verschoben. Zum Vergleich: gute Experimente
haben Auflösungen von 10 meV.

Quanten Monte-Carlo
Die elektronische Struktur wird gewöhnlich im sogenannten
Einteilchenbild betrachtet, d.h. die berechneten Eigenschaften sind die
eines einzelnen Elektrons in der Umgebung aller anderen
gleichartigen Elektronen. Wie schon erwähnt, kommen dann bei Bedarf
komplizierte Vielteilchenkorrekturen dazu. Da das nicht immer ausreicht,
gibt es seit kurzer Zeit auch für die Quantenmechanik von
Festkörperelektronen echte Vielteilchenrechnungen. Wegen ihres
statistischen
Zugangs heißen diese Methoden "Quanten Monte-Carlo-Verfahren".
Am Beispiel von
GaAs konnten damit sehr genau neben dem elektronischen Grundzustand und der
Gitterkonstanten erstmals auch Ladungsverteilungen und Bindungsvorgänge
betrachtet werden25-27.
Solche Rechnungen sind derzeit noch äußerst selten,
werden aber in Zukunft nach verbreiteter Ansicht eine große
Bedeutung haben,
wenn nicht sogar die Entwicklung dominieren.

Gruppe
Prof. Dr. W. Schattke; Dr. E.E. Krasovskii (Kiew) als häufiger Gast;
R. Bahnsen, Dr. A. Bödicker, S. Brodersen, Dipl.-Phys. J. Dittmer,
Dr. H. Eckstein,
Dipl.-Phys. N. Fitzer, Dr. R. Kaltefleiter,
Dipl.-Phys. A. Leventi-Peetz, Dipl.-Phys. S. Lorenz, Dr. D. Lukas,
Dipl.-Phys. J.-V. Peetz,
Dipl.-Phys. K.-W. Pieper,
Dipl.-Phys. C. Ramírez, M.Sc. E. Rodríguez, Dipl.-Phys. M.
Schilling,
Dipl.-Phys. C.-H. Solterbeck,
Dipl.-Phys. F. Starrost, Dipl.-Phys. T. Strasser, O. Tiedje;
kontinuierliche Absprache und Abgleich der Arbeiten mit der
experimentellen Arbeitsgruppe von Prof. Dr. M. Skibowski vor Ort
und weitere Zusammenarbeit mit den Gruppen von
H. Daimon (Osaka), C.S. Fadley (Berkeley und Davis),
W. Hackbusch (Kiel),
F. Liebau (Kiel), R. Redmer (Rostock), U. Simon (Essen), K. Terakura (Tsukuba)
und M.A. Van Hove (Berkeley).

Bibliographie
- E. E. Krasovskii, W. Schattke, The extended-LAPW-based k*p method for
complex bandstructure calculations, Solid State Commun.
93, 775 (1995)
- F. Starrost, S. Bornholdt, C. Solterbeck, W. Schattke,
Band-structure parameters by genetic
algorithm, Phys. Rev. B 53,
12549 (1996), Erratum Phys. Rev. B 54, 17226 (1996).
See also the poster.
- A. Bödicker and W. Schattke,
Nonlocal pseudopotentials in complex
bandstructure and photoemission calculations,
Phys. Rev. B 55, 5045 (1997)
- E. E. Krasovskii, W. Schattke, Surface electronic structure
with the linear methods of band theory, Phys. Rev. B, in press,
scheduled for 15No97
- R. Kaltefleiter,
Ortsraumrechnungen zur elektronischen Struktur von
Schichtkristalloberflächen,
Dissertation, Kiel (1997)
- M. Reigrotzki, M. Stobbe, R. Redmer, W. Schattke,
Impact Ionization Rate
in ZnS, Phys. Rev. B 52, 1456 (1995),
cond-mat/9504116
- M. Reigrotzki, N. Fitzer, S. S. Pennathur, R. Redmer,
W. Schattke, S. M. Goodnick,
Impact Ionization Rate in GaAs and ZnS,
in "Inorganic and Organic Electroluminescence", ed. by
R. H. Mauch and H.-E. Gumlich, Wiss. & Technik Verlag,
Berlin 1996, p. 39
- M. Reigrotzki, R. Redmer, I. Lee, S. S. Pennathur, M. Dür,
J. F. Wager, S. M. Goodnick, P. Vogl, H. Eckstein, W. Schattke,
Impact Ionization Rate and High Field Transport in ZnS
with Nonlocal Band Structure,
J. Appl. Phys. 80, 5054 (1996)
- S. Lorenz, C. Solterbeck, W. Schattke, J. Burmeister, and W. Hackbusch,
Electron scattering states at solid surfaces calculated with realistic
potentials, Phys. Rev. B 55, 13432 (1997),
cond-mat/9702118
- D. Samuelsen, W. Schattke, Electromagnetic Surface Response for
a Solid with
One-dimensional Crystallinity
Phys. Rev. B 51, 2537 (1995)
- A. Leventi-Peetz, E.E. Krasovskii, W. Schattke,
Dielectric Function and local
field effects of TiSe2, Phys. Rev. B 51,
17965 (1995)
- E. E. Krasovskii, O. V. Krasovska, W. Schattke,
Ab initio calculation of optical and photoelectron spectra of
KNbO3 and KTaO3, J. Electron Spectrosc. 83,
121 (1997)
- D. Lukas,
Ein quantenmechanischer und ortsraumnaher Ansatz
für die dielektrische Matrix eines halbunendlichen Kristalls
mit realistischer Oberfläche, Dissertation, Kiel (1996)
- A. Bödicker and W. Schattke,
Theoretical Photoemission Line Shapes
and Many Body Correlations, J. Electron Spectrosc. 76, 265 (1995)
- M. Traving, M. Boehme, L. Kipp, M. Skibowski, F. Starrost,
E. E. Krasovskii, A. Perlov, and W. Schattke,
Electronic structure of WSe2: A combined
photoemission and inverse photoemission study,
Phys. Rev. B 55, 10392 (1997)
- W. Schattke,
Photoemission within and beyond the
one-step model,
Progr. Surf. Sci. 54, 211 (1997)
- T. Strasser, F. Starrost, C. Solterbeck, W. Schattke,
Valence band photoemission from GaN(001)
and GaAs:GaN-surfaces,
Phys. Rev. B, in press, scheduled for 15No97
- C.-H. Solterbeck, W. Schattke, and C.S. Fadley,
Full-Hemisphere Valence
Band Photoemission Spectra Calculated for the Ideal Si(001)-Surface,
Surface Science 357-358, 245 (1996)
- A. Bödicker,
Vielteilcheneffekte und Photoemissionstheorie am
Beispiel des Schichtkristalls TiTe2,
Dissertation, Kiel (1996)
- C. Solterbeck, W. Schattke, J.-W. Zahlmann-Nowitzki, K.-U. Gawlik,
L. Kipp, M. Skibowski,
Azimuthal Dependence of GaAs(110) Ultraviolet
Photoemission Spectra, in "The Physics of Semiconductors",
ed. by M. Scheffler and R. Zimmermann, World Scientific,
Singapore 1996, Vol. 2, p. 835
- C. Solterbeck, W. Schattke, J.-W. Zahlmann-Nowitzki, K.-U. Gawlik, L. Kipp,
M. Skibowski, C. S. Fadley, M. A. Van Hove,
Energetic and
spatial bonding properties from angular distributions
of ultraviolet photoelectrons: application to the
GaAs(110) surface, Phys. Rev. Lett., in press, scheduled for 27No97,
cond-mat/9708218
- M.A. Van Hove, A.P. Kaduwela, H. Xiao, W. Schattke, and C.S. Fadley,
Application of Photoelectron Diffraction Theory to Circular Dichroism and
Spin-Polarized Photoelectron Emission, J. Electron Spectrosc. 80,
137 (1996)
- D. Samuelsen, W. Schattke, Photoemission by Screened Photon
Fields from Layered Solids, Surf. Sci. 327, 379 (1995)
- A. Bödicker, A. Leventi-Peetz, and W. Schattke,
Photoemission and
Photon Screening in Layered Crystals, J. Electron Spectrosc. 78,
481 (1996)
- H. Eckstein and W. Schattke, Variational
Quantum Monte Carlo Ground State of Lithium on a Slater orbital basis,
Physica A 216, 151 (1995)
- H. Eckstein, W. Schattke, M. Reigrotzki, R. Redmer,
Variational quantum Monte Carlo ground state of GaAs,
Phys. Rev. B 54, 5512 (1996),
mtrl-th/9607009
- H. Eckstein,
Quantenmechanische Monte-Carlo-Simulationen zum
Hochfeldtransport in Galliumarsenid, Dissertation, Kiel (1996)
|


![]()
![]()
