The combined analysis of valence photoelectron spectra and diffraction patterns

Web-proceedings of the
ALS Workshop on Theory and Computation for Synchrotron Applications



Traditional photoemission

As sketched in Fig. 1 several branches of photoemission spectroscopy in the vacuum ultraviolet (VUV) regime have developed and are still extending. There is a long history in quick and easy methods for the interpretation of photoemission spectra all of which are more or less approximations to the most accurate one-step model. The latter has been designed as a computer code during the 1970s by Pendry and since then has experienced many extensions, e.g. the application to non-muffin-tin potentials or to relativistic systems. The most direct access uses as a shortcut to the one-step model the identification of an angle integrated photoemission spectrum with the density of states (DOS). The DOS still is a valuable tool in the case of complicated systems where high quality surfaces cannot be prepared.


Fig. 1: Traditional and modern aspects of photoemission in the vacuum ultraviolet.


In the case of angle resolved spectra a correspondingly simple access is given by assuming direct, i.e. full momentum conserving, transitions. In fact the momentum perpendicular to the surface is not conserved leading to a serious failure of that procedure when demanding high resolution. This so called band mapping identifies peak positions in the electron distribution curve (EDC) with the binding energies of the initial states by momentum and energy conservation. Fig. 2 displays the differences between the actual energies and those obtained by experimental peak deconvolution algorithms applied to a spectrum calculated within the one-step model. An error bar of about 200 meV is unavoidable in a band-mapping analysis which in this example uses a whole set of most sophisticated deconvolution techniques as e.g. also the maximum entropy method.


Fig. 2: Accuracy of band mapping methods. Upper part: Valence (dotted) and conduction (solid) bands, the latter being shifted by the photon energy to lower energies; the bars denote the amplitudes the band enters the final state wavefunction. Lower part: Photoemission spectrum calculated from the above bandstructure; the bars are obtained in "theory" by marking all intersections of the valence bands with the conduction bands (direct transitions), in "experiment" by standard experimental deconvolution techniques of the theoretical spectrum.


The one-step model represents a complete calculation of the photocurrent within the golden-rule formula by using a one-electron bound state as initial state and an outgoing one-electron state describing also the solid-vacuum broken symmetry and the losses, the latter by an optical potential. The comparison of the spectra thus numerically obtained with the experimental ones yields the microscopic electronic structure such as the band structure, the crystal potential or magnetic properties by an optimization procedure. It determines those parameters still open in an ab-initio electronic structure calculation and it confirms or discredits the remaining ones. One has to keep in mind that actual band structures based on different ab-initio schemes are still at variance far above the experimental resolution. As an example for the presently achieved quality Fig. 3 shows for a new material of growing interest the normal emission EDC's where the careful analysis with one-step model calculations helped to associate the various peaks with definite initial states.1 For example, contrary to a first guess which attributed the high binding energy peak at -7.0 eV to a band edge the consideration of matrix elements in the theoretical calculation led to its identification as a surface state and to the "rehabilitation" of the theoretical ab-initio band structure. The latter predicted that band edge at a binding energy distinctly lower by 0.2 eV. Results of this kind are of eminent importance for understanding the binding and for providing a reliable basis to investigate more complicated phenomena as e.g. adsorption or electronic transport.


Fig. 3: Comparison between theoretical (left) and experimental spectra for normal emission from the GaN(001)1x1 surface; the matrix elements (below) are plotted vs. final state energy which is related to the photon frequency; they exhibit a dip at 35 eV that corresponds to the suppression of the -7 eV peak in the spectra near 44 eV photon frequency; this feature allowed the discrimination of a surface state from a band edge.


In the following, both last blocks in Fig. 1 characterizing some trends in the modern development of VUV-spectroscopy are discussed in turn.



Photoemission towards many-body effects

Fig. 4 displays some many-body effects currently under discussion for changing the photocurrent beyond the one-step model. It is represented by the photoemission vertex which symbolically decribes the golden rule formula if the corrections like the wavy and broken lines are omitted. The three lines of the triangle denote Green's functions that of the vertical line being attributed by its imaginary part to both initial states in the squared matrix element together with the energy delta function. The remaining lines denote the state of the escaping electron and its complex conjugate, resp., being excited by the light at the points where the wavy line enters the vertex.


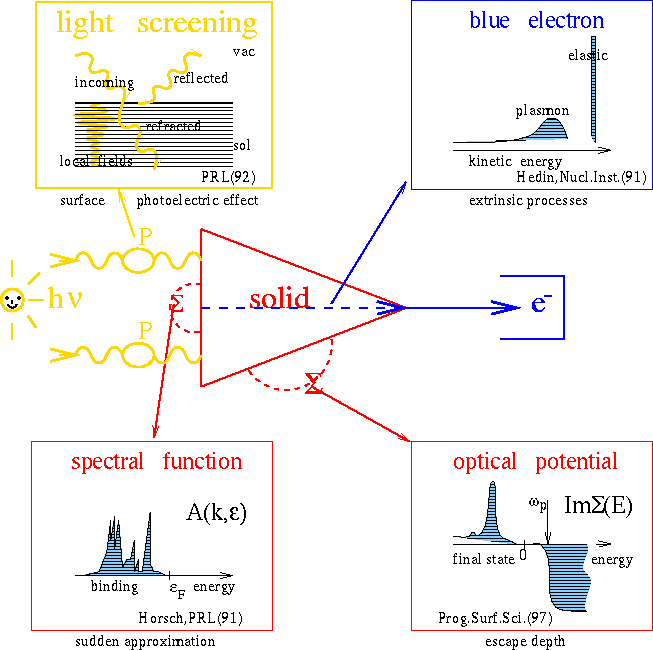Fig. 4: Photoemission towards many-body effects. Several many-body effects contributing to the photocurrent schematically drawn as corrections to the photoemission vertex, middle part; upper left: the exciting photon is deteriorated by surface and bulk induced response fields; upper right: inelastic effects like plasmon excitations add to the elastic part of extrinsic final state scattering; lower left: the final state structure is completely neglected in the sudden approximation, but the small energy scale of superconductivity features may justify the solely use of an initial state spectral function; lower right: the selfenergy determines the complete quasiparticle corrections, especially the hole life time and the final state optical potential.


Regarding the initial state a selfenergy correction can be introduced accounted for by using the many-body spectral density instead of the imaginary part of the bare, i.e. unperturbed solution of the one-particle Schrödinger equation. Neglecting all kinds of final state scattering the spectral function often is taken to represent the photocurrent, which is denoted as the "sudden" approximation. Frequently applied to superconductivity spectra it is claimed to be justified by the tiny energy scale superconductivity deals with.2 However, the neglected many-body effects might play on the same stage. Similarly, magnetic exchange can be considered in terms of the spectral function and a lot of investigations about spin dependent photoemission use this representation in a relativistic formulation, e.g. to investigate the magnetic bandstructure via magnetic linear dichroism.3

The bubbles introduced into the wavy lines represent the screening of the incident light by the solid and especially by its surface. The solid response is determined by calculating the full momentum and energy dependent dielectric function and inserting the polarization diagram. The surface response is connected with the so called surface photoelectric effect.4 Specifically sensitive to both are layered crystals, because their anisotropic structure allows to separate these effects which predominantly affect those states dispersing in surface perpendicular direction.5,6 Furthermore, large induced local fields arise near the plasma frequency in these materials.7

The selfenergy insertion into the final state Green's function is another representation for the optical potential. Its imaginary part stands for a rough collection of the losses the escaping electron suffers and is also described by the escape depth culminating in a vastly exploited empirical relation between that depth and the kinetic energy. A first ab-initio calculation8 in the GW-approximation of the self-energy is displayed in Fig. 5 and shows the typical behavior of the empirical formula with respect to the quadratic behavior near the Fermi energy and the strong increase near the plasmon threshold. The same figure also shows how strongly the photoemission spectra are affected by the self-energy insertions into both the initial and final states. With respect to high resolution spectroscopy these changes can hardly be tolerated.


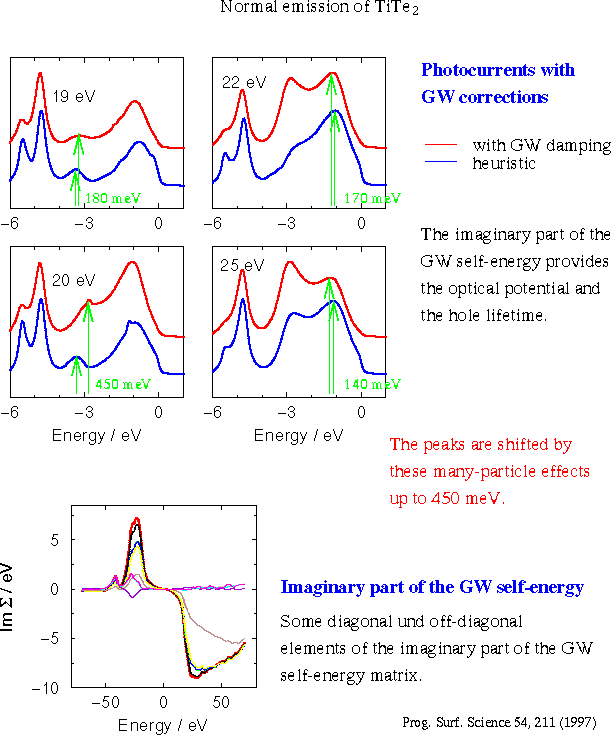Fig. 5: Ab-initio calculated selfenergy and its effect on the spectra; compared is with spectra whose hole life time and optical potential are adjusted to empirical constants frequently used in photoemission.


A further correction is sketched in Fig. 4 which actually mostly regards core level spectroscopy and which will be discussed at some other place of this workshop. The plasmon satellites surely will also influence the valence band spectra, however, to date it is completely unknown in what manner. The blue electron approach of Hedin9 insufficiently represented by the broken line dividing the vertex into two shows how intrinsic and extrinsic losses mix and make the sudden approximation rather valueless.

This and the whole zoo of mentioned and unmentioned many-body effects need photoemission investigations as their prominent investigative tool. For future research they are regarded less as spoiling the traditional photoemission investigation but rather as representing extremely interesting objects. The current development towards highest resolution opens the door to these challenges.



Full hemisphere

The last topic discussed here deals with the strongly increasing representation of photoemission results in two-dimensional patterns with respect to the surface parallel momentum space, partly as a collection of angular scans and partly as an instantaneous full hemisphere mapping of the photocurrent. The latter experienced an important impact by the development of suitable detectors.10,11 In Fig. 6 some topics dicussed in this context are listed.


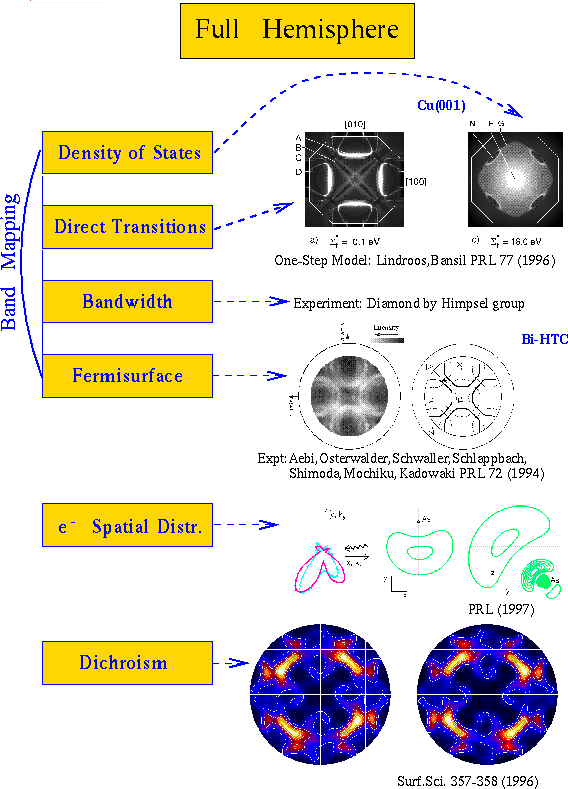Fig. 6: Some topics being discussed in connection with full hemisphere photocurrent acceptance: By varying the escape depth (selfenergy) the structure changes from a DOS like shape to direct transitions; visualization of the Fermi surface for a high temperature superconductor; identification of the emitting charge density of the dangling bond for the GaAs(110) surface; change of the emission pattern with polarization of the circularly polarized light.


For example, a specific procedure for determining the bandwidth is sketched in Fig. 7. This quantity is actually in discussion because of quasiparticle effects. Here, definite energetic configurations in momentum space are exploited with the help of two-dimensional representations. Generally, one of the aims is to directly visualize the bands and the surface DOS. At fixed energies of initial and final state the patterns show a lot of similarities with these quantities. However, for the reason stated above, they need the full calculation to yield a reliable interpretation. The patterns show different shapes in different Brillouin zones, they depend on the damping of the final state, and the lack or presence of emissions cannot be determined in advance.


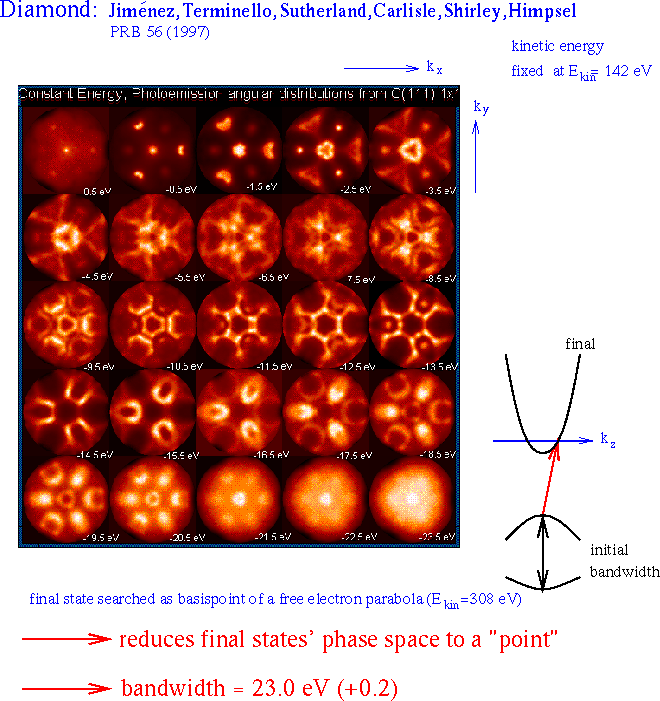Fig. 7: Determination of the bandwidth by confining the phototransition to the band edges of the valence and conduction bands.


Thus the experiment alone is only partly predictive. Calculations of that kind have been carried through in the one-step model and are in further progress.8,12,14 By a systematic treatment they hopefully will lead also to some sort of short-cut tools which dispense with the full theoretical calculation.13 At present it seems that the surface DOS comes closer to the emission patterns and that the band shapes, as e.g. the Fermi surface, are better resolved by using the traditional way. That means one has to look near the prominent spots for the maxima of the EDCs and has to take those for the estimated band energies. However, one of the main advantages is offered by an enhanced sensitivity of the patterns towards changes in the initial state energy which becomes analytically obvious in the case of bands with little dispersion.


Fig. 8: Contributions to the photoemission matrix element, a), c) final states for two different emission directions and b) initial state; for illustration of the surface atomic positions a frame is drawn; the product of initial and final state wavefunctions has to be integrated picking up only those regions where both are significantly different from zero; a strong localization arises from the final state's shape.


Another advantage emerges in the property of probing the spatial distribution of the valence charge at the VUV energies, see Fig. 8 The spatial structures of the final state wavefunction, i.e. especially regions of non-zero amplitude, project the initial state onto equivalent regions within the matrix element integration. Thus a specific probing of the spatial electron distribution of the initial state occurs. In a similar manner as the X-ray diffraction patterns (XPD) can be analyzed for the geometric configuration of the surface near ions, here the patterns represent parts of the valence charge accumulation. It is sketched in Fig. 9 how the charge density displayed in the pattern concentrates on space regions of increasingly higher localization with increasing kinetic energy of the probing electrons. Thus, sampling the energy from the VUV to the X-ray regime allows to get an image of the space and energy distribution of the bound electrons.13


Fig. 9: Emission from a backbond influenced state resolved for its contribution from different spatial regions as sketched in the right hand part by inner, middle, and outer; the inner contribution is negligible at this kinetic energy for VUV excitation, the middle area dominates above 500 eV and exclusively constitutes the current above 1 keV.


Progress could be achieved by investigating the circular dichroism of angular distributed electrons (CDAD) in close relation to the core level experiments. A change, especially a rotation of extended regions of the pattern, occurs due to the angular momentum transferred to the final states by the photon. Additionally, it is still more sensitive to the surface than usual photoemission.14 Fig. 10 shows a comparison of experiment and theory for the Si(001) surface. The emissions whose origin can be traced to the chains of tetrahedral bonds of the surface atoms with those below show a rotation of the pattern in close agreement with experiment. Two emissions which display an opposite rotational sense between theory and experiment are attributed to the binding chains of the surface atoms to the on-top dimers which has been neglected in theory by treating an ideal Si(001) surface in this first attempt.15

From these examples the full hemisphere investigations - quite common in XPD - seem to become an exciting new tool in the case of VUV valence band photoemission. It is because of its capability to unite the spatial or angular dependence with the energy dependence of the emissions in order to detect not only the energetic structure but also directly the wave function represented by the charge distribution.


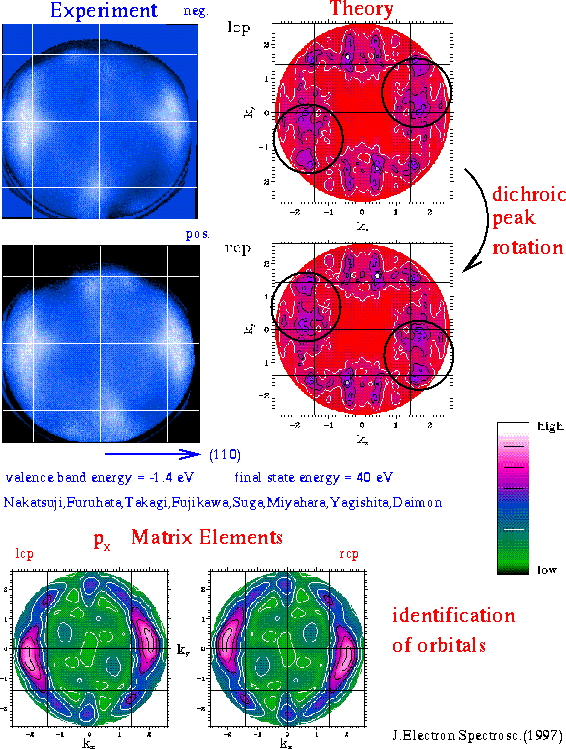Fig. 10: Circular dichroism for the valence bands of Si(001);the encircled high intensity parts rotate similarly to experiment for going from left to right hand circularly polarized light; the origin of these emissions is traced by considering the matrix elements to px orbitals; the emissions near kx=0 rotating oppositely to experiment are associated with py orbitals of the surface below (above) bonds in theory (experiment).




Conclusions

In conclusion probing many-body effects as well as imaging the wave function can be seen as most promising developments of valence band photoemission. The interface between experiment and theory, see Fig. 11, shows many connections, however, the actual state of the art demands full theoretical calculations for the interpretation as it is practised in the analysis of low energy electron diffraction (LEED) and XPD data. To ask only for a quick and easy interpretation of photoemission looks similar to relying entirely on imaging the optical LEED without analysis of I(V) curves or on using exclusively forward and backward scattering for the XPD analysis.


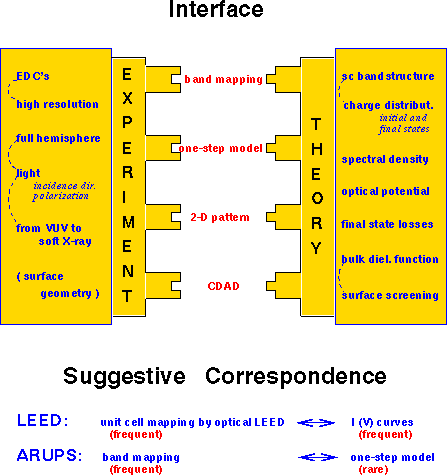Fig. 11: Sorry for listing only 4 pins of the interface connector




Acknowledgement

Continuous cooperation in this field with M. Skibowski, E.E. Krasovskii, C.S. Fadley, M.A. van Hove, H. Daimon, C. Solterbeck, F. Starrost, and T. Strasser is gratefully acknowledged. The work was supported by the Bundesministerium für Bildung, Wissenschaft, Forschung und Technologie (Project No. 05 605 FKA).

References

  1. T. Strasser, F. Starrost, C. Solterbeck, W. Schattke, Phys. Rev. B 56, 13326 (1997)
  2. S. Horsch, Phys. Rev. Lett. 66 (1991) 2258
  3. A. Rampe, G. Güntherodt, D. Hartmann, J. Henk, T. Scheunemann, R. Feder, Phys. Rev. B (1997) to be published
  4. F. Forstmann, R. Gerhardts, Metal Optics Near the Plasma Frequency, ed. G. Höhler, Springer Tracts in Modern Physics Vol. 109 (Springer, Berlin, 1986)
  5. D.Samuelsen, E.Pehlke, W.Schattke, O. Anderson, R. Manzke, M. Skibowski, Phys. Rev. Lett. 68 (1992) 522
  6. A. Bödicker, A. Leventi-Peetz, W. Schattke, J. Electron Spectrosc. Relat. Phenom. 78 (1995) 481
  7. A. Leventi-Peetz, E.E. Krasovskii, W. Schattke, Phys. Rev. B 51 (1995) 17965
  8. W. Schattke, Prog. Surf. Sci. 54 (1997) 211
  9. L. Hedin, Nucl. Instruments and Methods in Phys. Res. A 308 (1991) 169; T. Fujikawa, L. Hedin, Phys. Rev. B 40 (1989) 11507
  10. H. Nishimoto, H. Daimon, S. Suga, Y. Tezuka, S. Ino, I. Kato, F. Zenitani, and H. Soezima, Rev. Sci. Instrum. 64 (1993) 2857
  11. I. Jiménez, L.J. Terminello, D.G.J. Sutherland, J.A. Carlisle, E.L. Shirley, F.J. Himpsel, Phys. Rev. B 56 (1997) 7215
  12. M. Lindroos, A. Bansil, Phys. Rev. Lett. 77 (1996) 2985
  13. C. Solterbeck, W. Schattke, J.-W. Zahlmann-Nowitzki, K.-U. Gawlik, L. Kipp, M. Skibowski, C.S. Fadley, M.A. Van Hove, Phys. Rev. Lett. 79, 4681 (1997)
  14. C.-H. Solterbeck, W. Schattke, C.S. Fadley, Surf. Sci. 357-358 (1996) 245
  15. K. Nakatsuji, H. Daimon, T. Furuhata, H. Takagi, M. Fujikawa, S. Suga, T. Miyahara, A. Yagishita, C.-H. Solterbeck, W. Schattke, J. Electron Spectrosc. Relat. Phenom. (1997) accepted

Wolfgang Schattke
CAU Kiel
Physics
Theory
Home
Frontiers
4.2.1998