Even today the proper theoretical treatment of solid surfaces as interacting
inhomogeneous quantum systems remains a formidable task. While Quantum Monte Carlo
calculations for solids are state of the art by now, the application to solid
surfaces is a rather new area of current research.
Here we present some highlights of our results. Full details can be found
in a recent
publication.
We apply the variational
quantum Monte Carlo method to the (110) surface of galliumarsenide.
The variational parameters in the many-body trial wave function are minimized
according to Ritz' rule the lower the energy the better the wave function.
Some of these parameters influence the localization of the electrons to the whole surface
system: Due to the repulsive electron-electron interaction the electrons want to
drift into the vacuum, thereby lowering the total energy. But simultaneously the
attractive electron-ion interaction decreases, leading to an increasing total energy.
These two competing effects will lead to an optimal equilibrium distribution
of the electron density with the lowest energy.
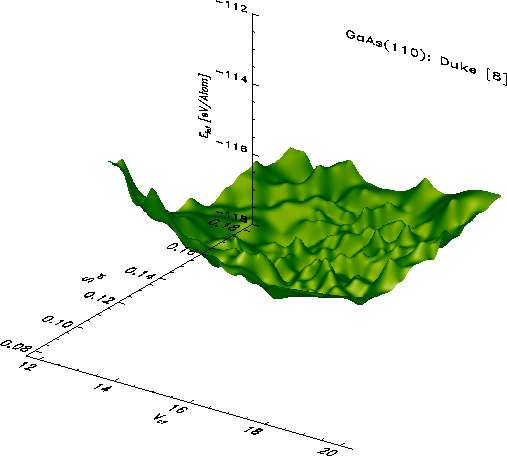
Typical energy landscapes for the GaAs(110) surface in the ideal(red) resp.
Duke(green) model are shown in the following two pictures. Despite
statistical noise a minimum is clearly resolvable. The x- and y- coordinates
of the point of lowest energy give the optimal
many-body wave function.

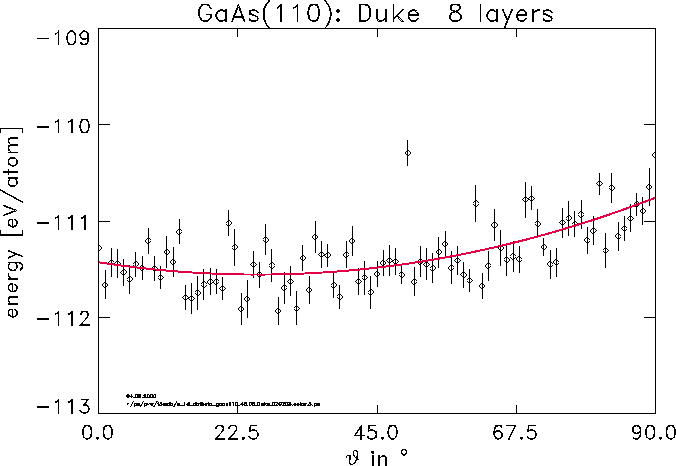
Even more detailed information about the behavior of the electrons at the
surface can be gained. E. g. the angle of the so called dangling
bond orbital is unknown a priori. In the final picture the
dependence of the total energy from this variational parameter for GaAs(110) in
the Duke model is shown.
Despite huge statistical noise in the QMC data an optimal value of 26 degree
can be determined with the help of a statistical fit.
See also:
QIRM Package available for download.


![]()
![]()
